Getallen met twee decimalen

Kommagetallen worden op de basisschool vaak in groep 6 als onderdeel van het rekenen geïntroduceerd. Vaak in de context van geld of meten. In groep 7 komt rekenen met twee decimalen (zoals 2,45) aan bod, en leren kinderen ook delen en vermenigvuldigen met kommagetallen. In groep 8 wordt dit verder verdiept en uitgebreid.

Allemaal hartstikke leuk, maar waarom deze blog? Omdat het voor een kind best lastig kan zijn, om zich een voorstelling te maken van bijvoorbeeld 3 honderdsten. En het is wel fijn (zacht uitgedrukt) om te snappen wat je opschrijft, toch? Hoe je kind inzicht krijgt in decimale getallen en zijn getalbegrip kan vergroten, lees je hier!

HOEVEEL DECIMALEN?!

Een getal kan oneindig veel decimalen hebben. Kijk maar eens naar dit getal:

Hoeveel cijfers staan hier achter de komma?! Veel. Te veel. Ik houd het in deze blog dus maar even bij twee cijfers achter de komma.

Het is belangrijk om het verschil te zien tussen een kommagetal en decimalen:

• Een kommagetal is het hele getal mét komma, bijvoorbeeld 3,14.

• Decimalen zijn alleen de cijfers achter de komma, dus in 3,14 zijn dat 1 en 4.

GETALLEN VÓÓR DE KOMMA

Hoe is het getalbegrip van je kind? Kent hij de posities van de honderdtallen, duizendtallen en tienduizendtallen? Misschien weet je dat niet zo goed. Het is gemakkelijk te achterhalen. Schrijf het onderstaande getal op en vraag hoe de posities van de getallen heten.

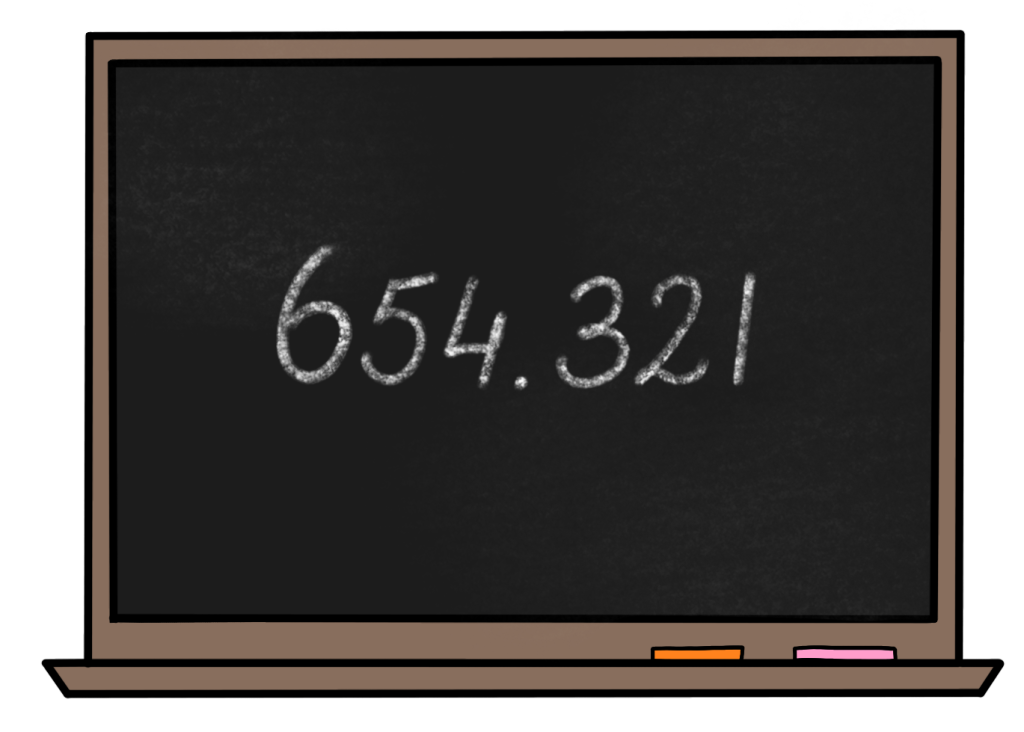
De 1 in dit getal staat op de plek van de enen. 
De 2 op de plek van de nee… niet van de tweeën. Van de tientallen. 
De 3 van de honderdtallen, 4 van de duizendtallen, 5 van de tienduizendtallen en 6 van de honderdduizendtallen. 
Hier stop ik, hoor. Anders komen we bij de miljoenen. Daar schrijf ik wel weer een andere keer een blog over.

DE GETALLEN ÁCHTER DE KOMMA

In deze blog heb ik het niet over het getal vóór de komma, maar over de posities van de cijfers áchter de komma. Die hebben ook een naam. Vraag je kind maar eens of hij de namen kent. Zo niet, dan kun je het aan hem vertellen. Ik gebruik voor dit voorbeeld het volgende getal:

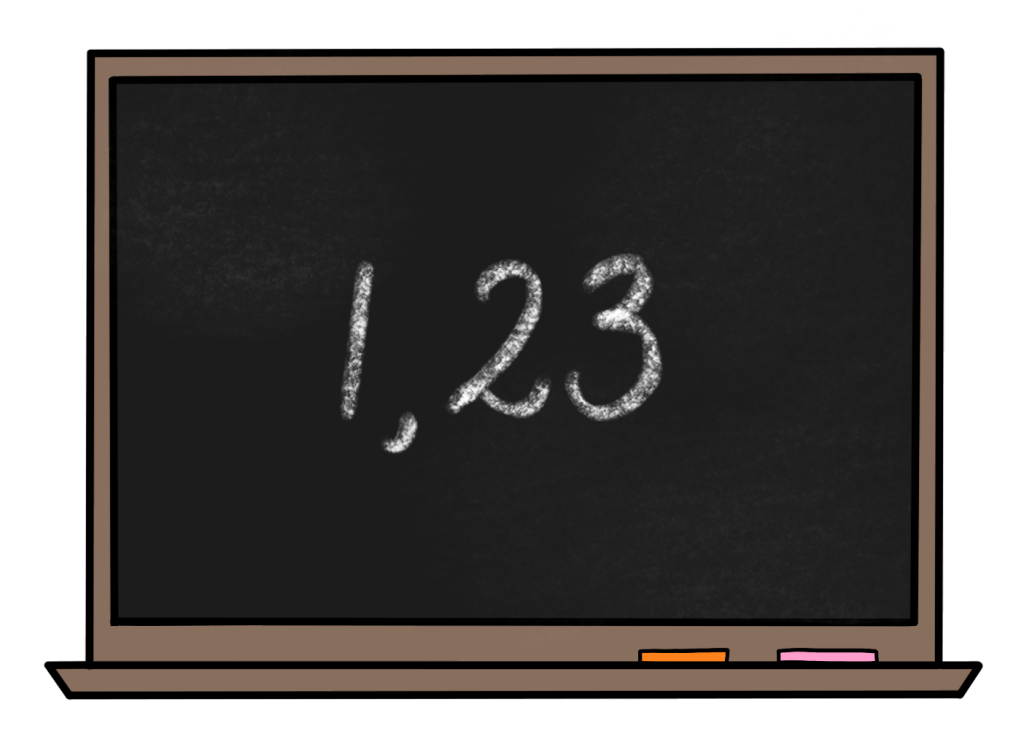
De 2 in dit getal staat op de plek van de ‘tienden’ en de 3 op de plek van de ‘honderdsten’. 

TIENDEN EN HONDERDSTEN

Waarom heten de getallen achter de komma zo, tienden en honderdsten? Dat zal ik uitleggen! 

Ik gebruik het getal 0,1. Dit is 1 tiende (1/10). De 0,1 (1/10) past 10 keer in een hele (dus in het getal 1). 

Nu het getal 0,01. Dit is 1 honderdste (1/100). Drie keer raden hoe vaak deze in een hele (dus in het getal 1) past! Dat is 100 keer. 

TIENDEN EN HONDERDSTEN IN BREUKEN

Weet je kind ook dat 1 tiende er als breuk zo uitziet: 

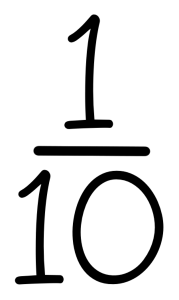
En ook dat 1 honderdste er dan zo uitziet:

DE BETEKENIS VAN DE GETALLEN ACHTER DE KOMMA

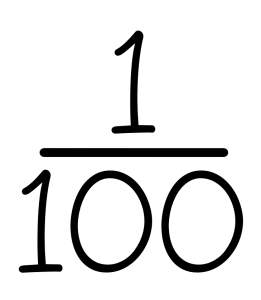
Bij getallen vóór de komma is het makkelijker, om je er een voorstelling van te maken. Als je het getal 4 ziet, dan denk je misschien aan 4 peren. 

Hoppa! 4 peren. Duidelijk. Maar 0,1… uhhh… peer? Of 1/100 peer..? Ja, hier raak je mij zelfs kwijt.

DECIMALEN BIJ GELD

Als je wilt uitleggen, wat de getallen achter de komma betekenen, is het niet echt handig om een peer als voorbeeld te nemen. Ik gebruik voor dit voorbeeld liever geld.

Zoals je kind misschien nog weet, kun je 0,1 ook als 0,10 schrijven. (In rekenles 32 van groep 6 leg ik uit, waarom dat zo is.) Het getal 0,10 verander ik in €0,10 / 10 cent. Hoe vaak past 10 cent in een hele euro? Dat is 10 keer. 

De 0,01 verander in €0,01 (1 cent). Hoe vaak past die in een hele euro? Dat is 100 keer! 

Nu kan hij zich vast al een betere voorstelling van 1 tiende en 1 honderdste maken.

REKENEN MET KOMMAGETALLEN

Als je kind dit begrijpt, kan hij een begin maken met het rekenen met kommagetallen. Hoe verandert een getal, als je sprongen van 0,1 (oftewel 0,10) maakt? 

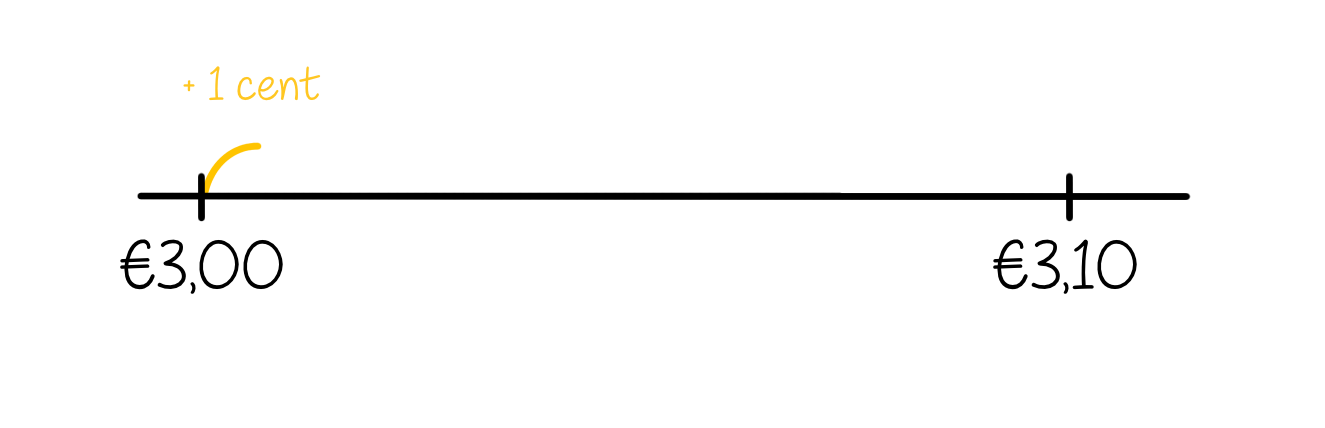
Begin bij €3,00. Bij welk getal kom je uit als je met tien cent (oftewel een tiende) verder springt? En daarna?

Kan je kind ook sprongen van 1 cent (oftewel een honderdste) maken? Hij zal zien, dat dit een stuk langzamer gaat dan de sprongen van 0,1. Je kunt het iets moeilijker maken door te vragen in hoeveel sprongen hij bij €3,10 is.

GETALBEGRIP

Getalbegrip begint, zodra een kind gaat tellen. Naarmate de getallen groter (8.973.145) en kleiner (0,678) worden, neemt het getalbegrip bij een kind vaak af. Best wel logisch, want kun jij je een goede voorstelling maken bij deze getallen? Lastig, hè! Een kind kan het als een brei van getallen zien. En dat maakt het rekenen natuurlijk niet leuker. Des te belangrijker om dit voor te zijn! Geef de getallen betekenis en zorg er op die manier voor dat je kind plezier in het rekenen blijft behouden!

Psst… over kommagetallen heb ik nóg een interessant blog geschreven. Wil je je kind verder helpen? Neem dan een kijkje op het blog ‘Kommagetallen – tienden en honderdsten’.

REKENLESSEN OP VIDEO

Op lesvananne.nl vind je meer dan 300 rekeninstructies op video! Natuurlijk heb ik ook rekenvideo’s over kommagetallen gemaakt. Je vindt ze op de pagina’s met de rekenlessen van groep 6 en groep 7 en groep 8. 

GROEP 6 LES 32 Het kommagetal
GROEP 6 LES 34 Kommagetallen bij het wegen
GROEP 6 LES 53 Kommagetallen bij het meten

GROEP 7 LES 7 Keersommen met komma onder elkaar
GROEP 7 LES 10 Getallen met twee decimalen
GROEP 7 LES 19 Kommagetallen delen door 10 en 100
GROEP 7 LES 21 Maten met komma omrekenen
GROEP 7 LES 23 Van breuk naar kommagetal

GROEP 8 LES 1 Van gemengd getal naar kommagetal
GROEP 8 LES 3 Kommagetallen vermenigvuldigen
GROEP 8 LES 5 Kommagetallen afronden
GROEP 8 LES 8 Kommagetallen door elkaar delen

KOMMAGETALLEN OP YOUTUBE

Ook op YouTube vind je een aantal van onze rekenvideo’s over kommagetallen. Leuk als je gelijk een kijkje neemt en helemaal leuk als je op een duimpje omhoog onder de video klikt!