Grote getallen delen: 3 rekenstrategieën

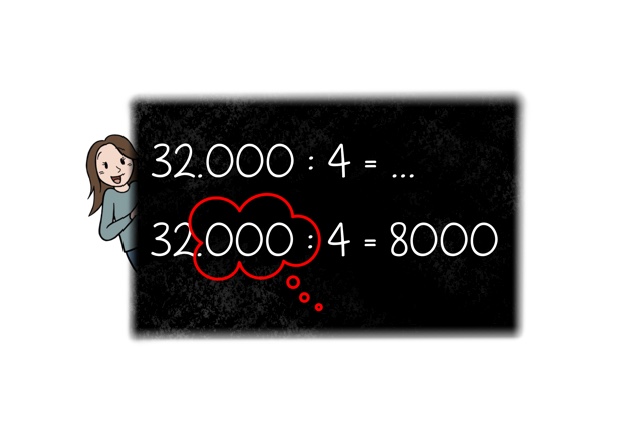
Blijft je kind maar naar de rekensommen staren, zonder te weten wat hij kan doen om hem op te lossen? Is je kind soms langer dan de andere kinderen met de rekenles bezig? 

Vaak heeft het te maken met het niet weten welke rekenstrategie er toegepast kan worden. In deze blog zet ik 3 rekenstrategieën op een rij, die gebruikt kunnen worden bij het delen van grote getallen. Zo weet jouw kind straks ook, hoe hij de rekensommen kan oplossen!

Rekenstrategie 1: Nullen weghalen

Laat ik beginnen met het delen van getallen door 10, 100 en 1000. Delen door 10, 100 en 1000 is een makkie als het getal, waardoor je het wilt delen, op nullen eindigt. Neem de volgende som: 

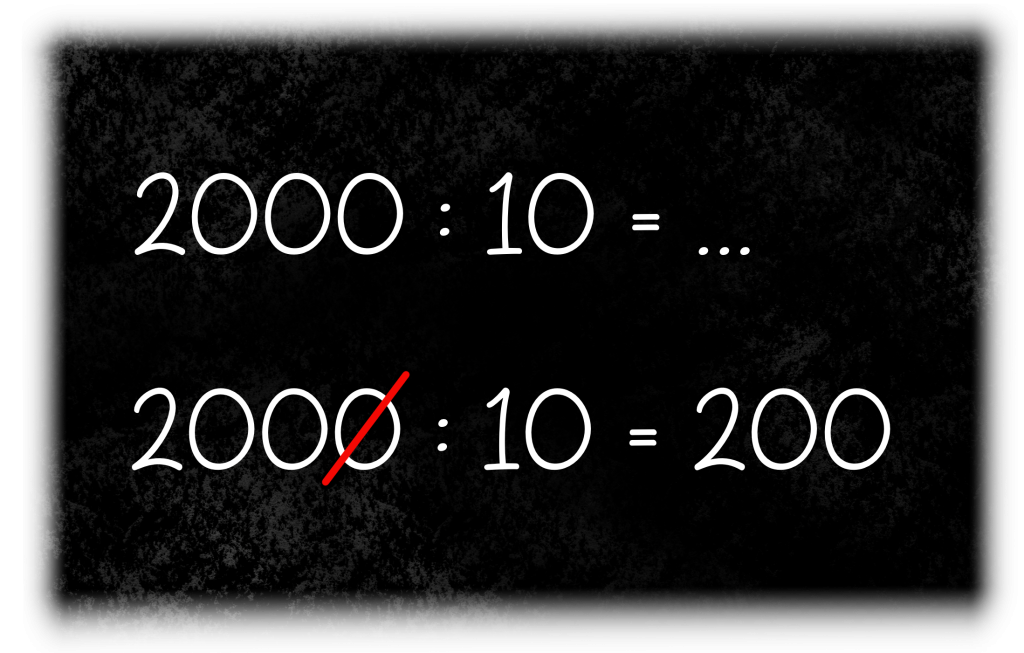
Nu denk je misschien: “Zo, zo, 2000 is best een groot getal. Hoe kan ik dat getal door 10 delen?”

Heel simpel! Bij getallen die je door 10 deelt, verdwijnt een 0 aan het eind. 2000 gedeeld door 10 is dan… 200!

Nog een voorbeeld:

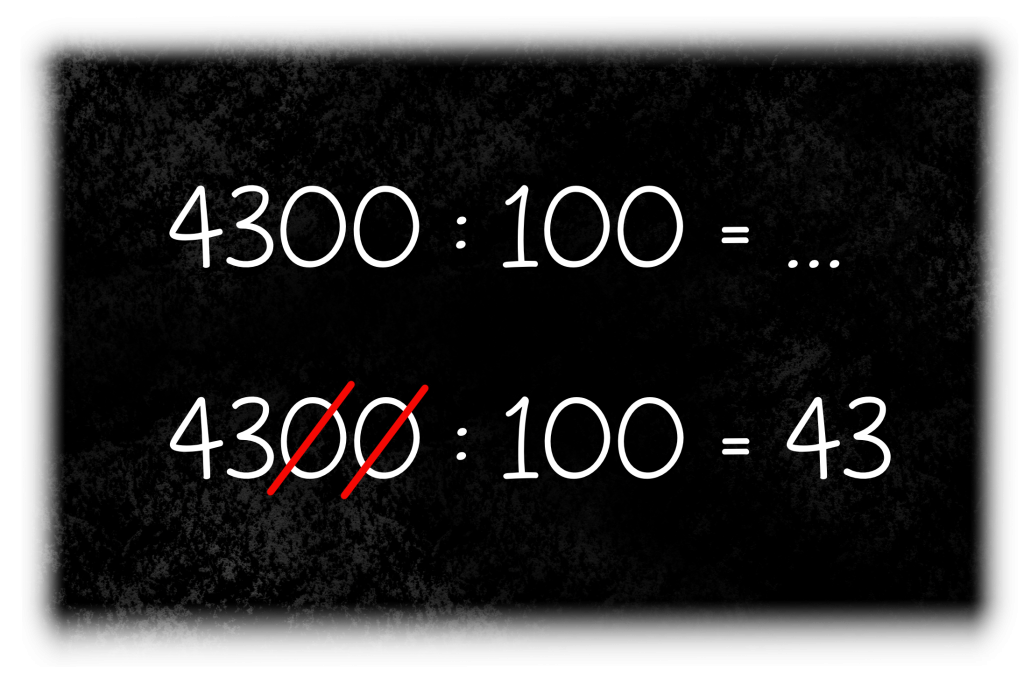
Misschien denk je: “Jaaa, nu wordt het echt lastig!” Helemaal niks van waar! Bij getallen, die je door 100 deelt, verdwijnen aan het eind twee nullen aan het eind. Dan is 4300 gedeeld door 100… 43!

Nu kun je vast wel raden wat er gebeurt, als je een getal door 1000 deelt. Er verdwijnen 3 nullen. Wat is het antwoord dan op 58.000 : 1000..?

Rekenstrategie 2: Nullen wegdenken (en later weer opschrijven)

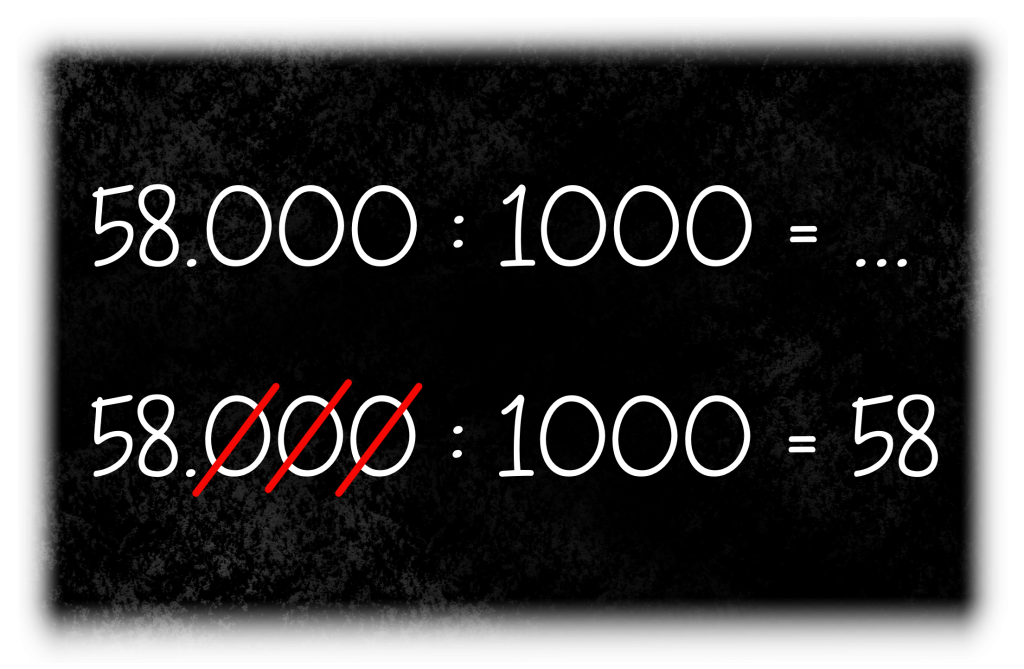
Maar wat nou als je een getal niet door 10, 100 of 1000 moet delen, maar bijvoorbeeld door 4. Zoals bij de som 32.000 : 4.

Nu kunnen er geen nullen weggehaald worden. Je kunt de nullen wel wegdénken. 

Als je de nullen wegdenkt, wordt de nieuwe som 32 gedeeld door 4. Het antwoord daarop is 8. De nullen, die je net wegdacht, schrijf je nu weer achter het antwoord. Er komen dus drie nullen achter het antwoord. 

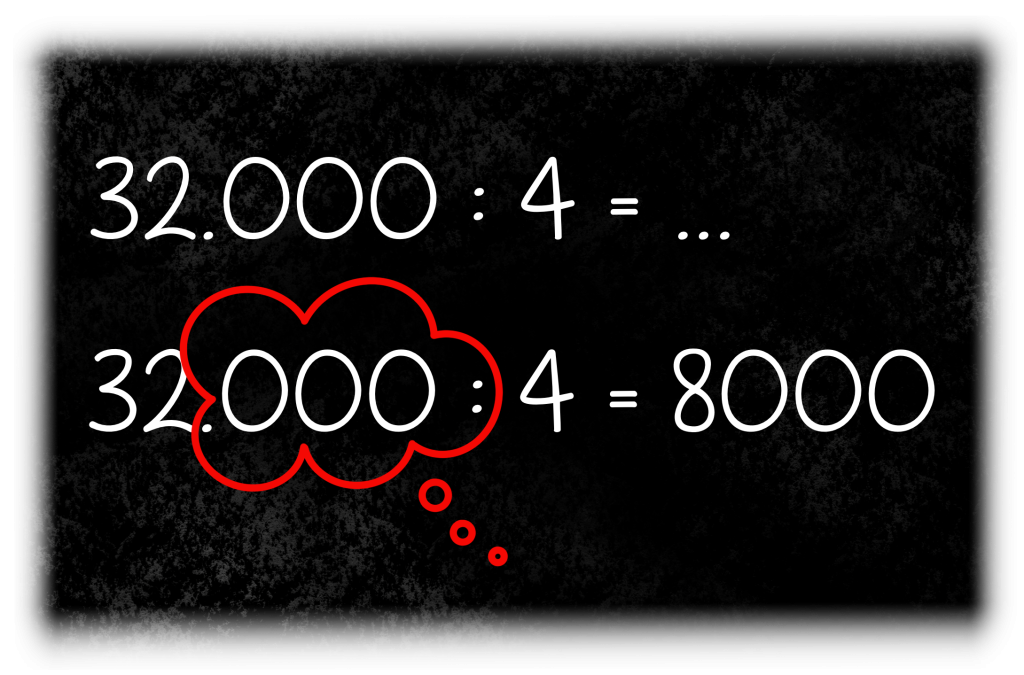
Et voilà, klaar is Kees! Uh… Anne.

Rekenstrategie 3: Nullen tegen elkaar wegstrepen

Voor een ander voorbeeld, is een andere strategie nodig. Voor het volgende voorbeeld gebruik ik de som 3500 : 500.

Dit keer kun je de nullen ‘tegen elkaar wegstrepen’. Daar bedoel ik mee, dat je voor iedere nul die je bij het ene getal weghaalt, je ook een nul bij het andere getal weg moet halen. 

Bij de 500 kun je twee nullen weghalen. Die moeten nu ook bij de 3500 weggehaald worden. De som verandert nu in 35 gedeeld door 5. Dat is… 7.

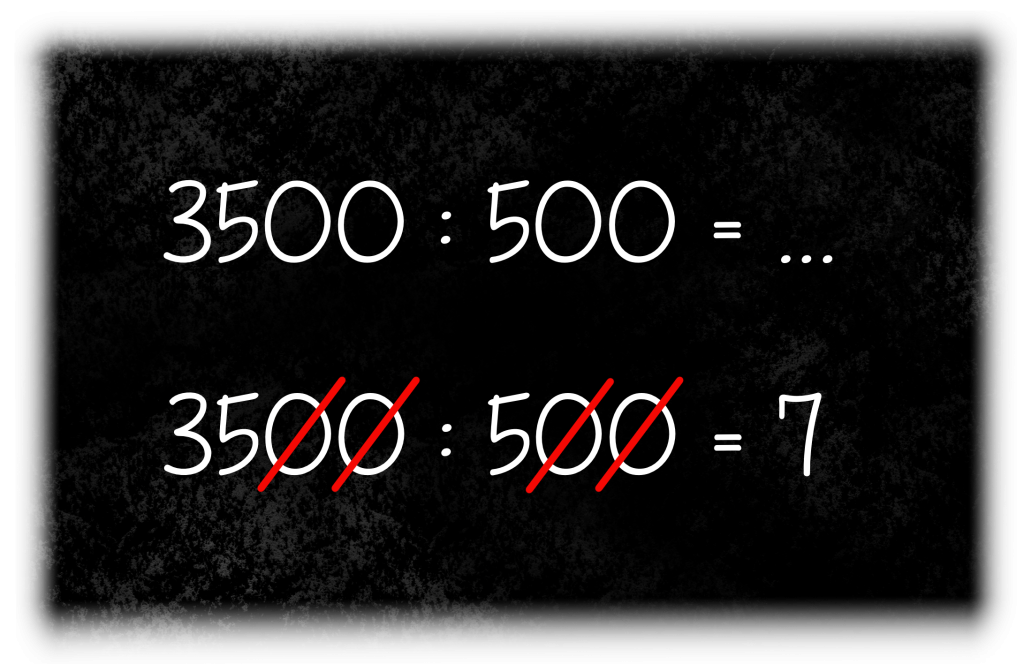
En nu? 

Niks! 

Wat? Niks?!

Ja, niks.

Bedoel je helemaal niks?

Ja! Je hoeft nu niks meer te doen. Alhoewel… ik raad je aan om het antwoord nog even te checken. Dat kun je doen door de deelsom in een keersom te veranderen. Gebruik de laatste twee getallen van de deelsom en maak daar een keersom van.

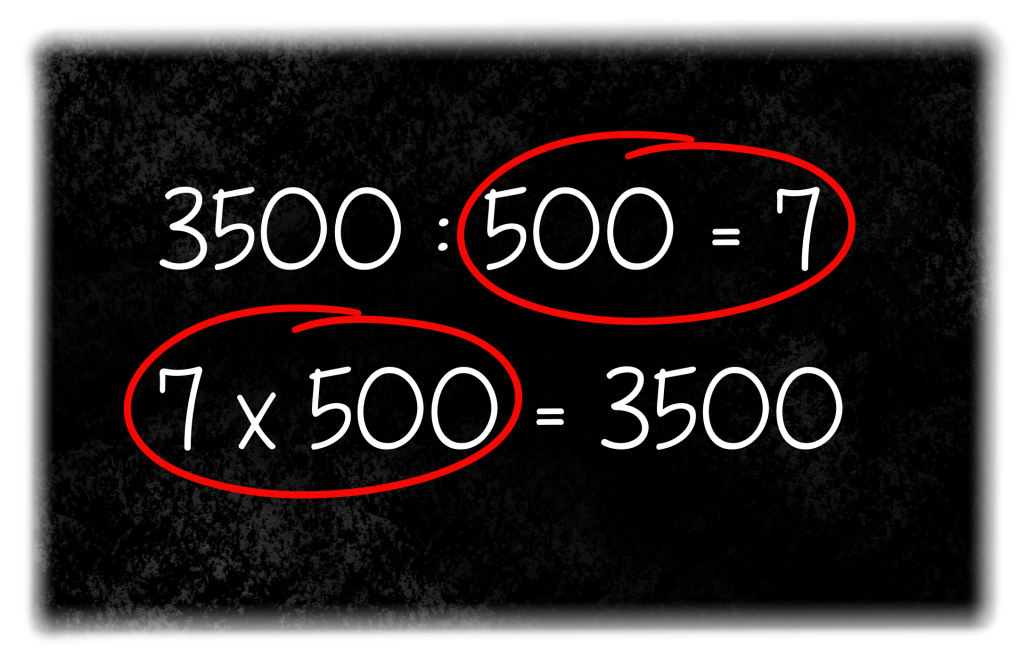
Het antwoord is 3500. Nu weet je zeker, dat het antwoord op de deelsom klopt. Als je nullen tegen elkaar wegstreept, hoef je daarna dus echt niets meer te doen! Behalve… het antwoord even checken met een keersom.

Wanneer leer je een rekenstrategie aan?

Tot slot, maar zéker niet onbelangrijk: wanneer leer je een rekenstrategie aan?

Strategieën worden aangeleerd als het begrip er is. Tenminste, dat zou in de ideale wereld gebeuren… Als een kind geen idee heeft hoe een getal samengesteld is (tientallen en eenheden), de waarde van een getal niet kent, nog niet weet wat plus, min, keer of gedeeld door betekent, dan is er eerst ander werk aan de winkel.

Lukt dit allemaal al wel goed? Dan is het tijd om aan de manier van uitrekenen (de strategie dus) en het tempo te werken.

Rekenlessen over delen

Heeft jouw kind extra uitleg bij de rekencategorie delen nodig? Vind je het prettig als een echte juf de rekenstof uitlegt? De onderstaande rekenlessen gaan over de categorie delen. Meld je aan en ga gelijk met deze rekeninstructies aan de slag!

GROEP 3 LES 25 Verdelen

GROEP 4 LES 41 Verdelen
GROEP 4 LES 47 Verdelen met rest

GROEP 5 LES 8 Delen
GROEP 5 LES 10 Verband keer en delen
GROEP 5 LES 35 Splitsend delen
GROEP 5 LES 50 Delen met tientallen
GROEP 5 LES 55 Delen met rest

GROEP 6 LES 7 Rekenen met getallen t/m 5000
GROEP 6 LES 9 Splitsend delen
GROEP 6 LES 31 Geldbedragen delen
GROEP 6 LES 44 Delen met getallen boven de 100
GROEP 6 LES 59 Grote getallen delen

GROEP 7 LES 17 Staartdelingen met rest
GROEP 7 LES 19 Kommagetallen delen door 10, 100 en 1000
GROEP 7 LES 32 Getallen delen door kommagetallen
GROEP 7 LES 33 Kommagetallen delen door helen

GROEP 8 LES 8 Kommagetallen door elkaar delen
GROEP 8 LES 11 Hele getallen delen door breuken
GROEP 8 LES 13 Getallen delen door gemengde getallen
GROEP 8 LES 15 Splitsend delen

Rekenlessen over delen op YouTube

Ken jij mijn YouTube-kanaal al? Daar zijn allerlei rekeninstructies te vinden. Zo krijg je alvast een indruk van de lessen die je op deze website vindt.

Over delen staan de volgende video’s op YouTube. Ik zou het leuk vinden als je onder de video een duimpje omhoog steekt! Veel rekenplezier!