Ezelsbruggetjes bij het rekenen

Door het gebruik van ezelsbruggetjes kun je gemakkelijker iets onthouden of toepassen. Waarom werken ezelsbruggetjes zo goed? En welke ezelsbruggetjes kun je toepassen tijdens het rekenonderwijs?

Waarom werkt een ezelsbruggetje?

Een ezelsbruggetje is een onthoud-techniek, een geheugensteuntje, een rijmpje of een vuistregel om iets heel makkelijk te kunnen onthouden. De reden dat een ezelsbruggetje zo goed werkt, is omdat er een verbinding wordt gemaakt in de hersenen die makkelijk op te halen is. Er wordt dus een structuur voor iets, dat je voorheen niet goed kon onthouden, gecreëerd.

Zulke geheugensteuntjes noem je ook wel mnemotechnieken (ja, dit is echt een woord). Het ezelsbruggetje heeft doorgaans niks te maken met datgene wat je moet onthouden.

Waar komt het ezelsbruggetje vandaan?

Wat heeft een ezel met geheugensteuntjes te maken?

De naam ‘ezelsbruggetje’ is afgeleid van het Latijnse ‘pons asinorum’, dat letterlijk ‘de brug van ezels’ betekent. In de bergen werden veel bruggen voor ezels gemaakt, door planken over ravijnen te leggen en om dus letterlijk de weg korter te maken. Een ezelsbruggetje is dus een kortere weg naar de bestemming.

Ezelsbruggetjes bij het rekenen

Welke ezelsbruggetjes worden in het basisonderwijs bij het rekenen gebruikt? Ik heb ze op een rijtje gezet!

Lengtematen

Wat is langer? Een meter of een decimeter?

Tijdens het rekenen krijgen de kinderen te maken met de lengtematen en de afkortingen daarvan. Om de verhoudingen tussen de maten goed uit elkaar te houden, zodat je er ook mee kunt rekenen is het belangrijk om ze in de goede volgorde te onthouden.

Een handig ezelsbruggetje is de zin: Kan Het Dametje Met De Centimeter Meten?

Kan = Kilometer (km)
Het = Hectometer (hm)
Dametje = Decameter (dam)
Met = Meter (m)
De = Decimeter (dm)
Centimeter = Centimeter (cm)
Meten = Millimeter (mm)

Pssst… Benieuwd naar hoe je zelf met je kind kunt oefenen met meten? Dat lees je in het blog ‘Oefenen met meten‘.

Hoeveel dagen hebben de maanden?

Veelal leren kinderen in groep 5 rekenen met de kalender, met de maanden en de dagen.

Leerdoel SLO (landelijk): Ik kan op een maand- en jaarkalender data en dagen aflezen en hierbij vragen over tijdsperiodes tussen data beantwoorden.
Bijvoorbeeld: Het is 6 november, over precies een half jaar moet ik weer naar de tandarts, wanneer is dat? Het is vandaag dinsdag 25 september, welke datum is het over precies twee weken?

Om met de kalender te rekenen, is het handig om te weten hoeveel dagen een maand heeft. Als ezelsbruggetje kun je je handen gebruiken. Hoe dan? Zo:

Wanneer je van je handen een vuist maakt, zie je de knokkels. Een hoge knokkel (berg) staat voor een maand met 31 dagen en de ruimte tussen de knokkels (dal) staat voor een maand met 30 dagen (en als uitzondering de maand februari met 28 of 29 dagen).

Laat je kind de maanden in goede volgorde opnoemen en tegelijkertijd een knokkel (berg) en de ruimte tussen knokkels (dal) aanwijzen. Laat je kind eerst naar de eerste knokkel (berg) wijzen en ‘januari’ zeggen. Vervolgens mag hij naar het dal ernaast wijzen en de volgende maand ‘februari’ opzeggen. Omdat januari een berg is, heeft januari 31 dagen, februari is een dal en heeft, de uitzondering op de regel, 28 of 29 dagen. Zo ga je verder tot je bij de maand komt, waarvan je het aantal dagen wilt weten.

Windrichtingen

Vaak leren kinderen in groep 6 de windrichtingen noord, oost, zuid en west.

Leerdoel SLO (landelijk): Ik ken de windrichtingen noord, oost, zuid, west en begrijp dat deze kunnen worden gebruikt om een plaats te bepalen of een route te beschrijven.
Bijvoorbeeld: Arnhem ligt in het Oosten van Nederland.

Belangrijk is om de windrichtingen in de goede volgorde te onthouden. Een handig ezelsbruggetje kan de zin zijn: Nooit Opstaan Zonder Wekker.

Nooit = Noord
Opstaan = Oost
Zonder = Zuid
Wekker = West

Handig om je kind te vertellen: De windrichtingen kun je in goede volgorde met de klok mee opschrijven.

Delen door en vermenigvuldigen met nul

3 x 0 = ..?
Er zijn best wat kinderen, die 3 zouden antwoorden.

15 : 0 = ..?
En hier wordt het antwoord 0 vaak genoemd.

Maar… Een keersom met nul is flauwekul, dit antwoord is namelijk altijd nul!

En… Delen door nul is flauwekul, delen door niks kan namelijk niet.

Sommen met verschillende bewerkingen

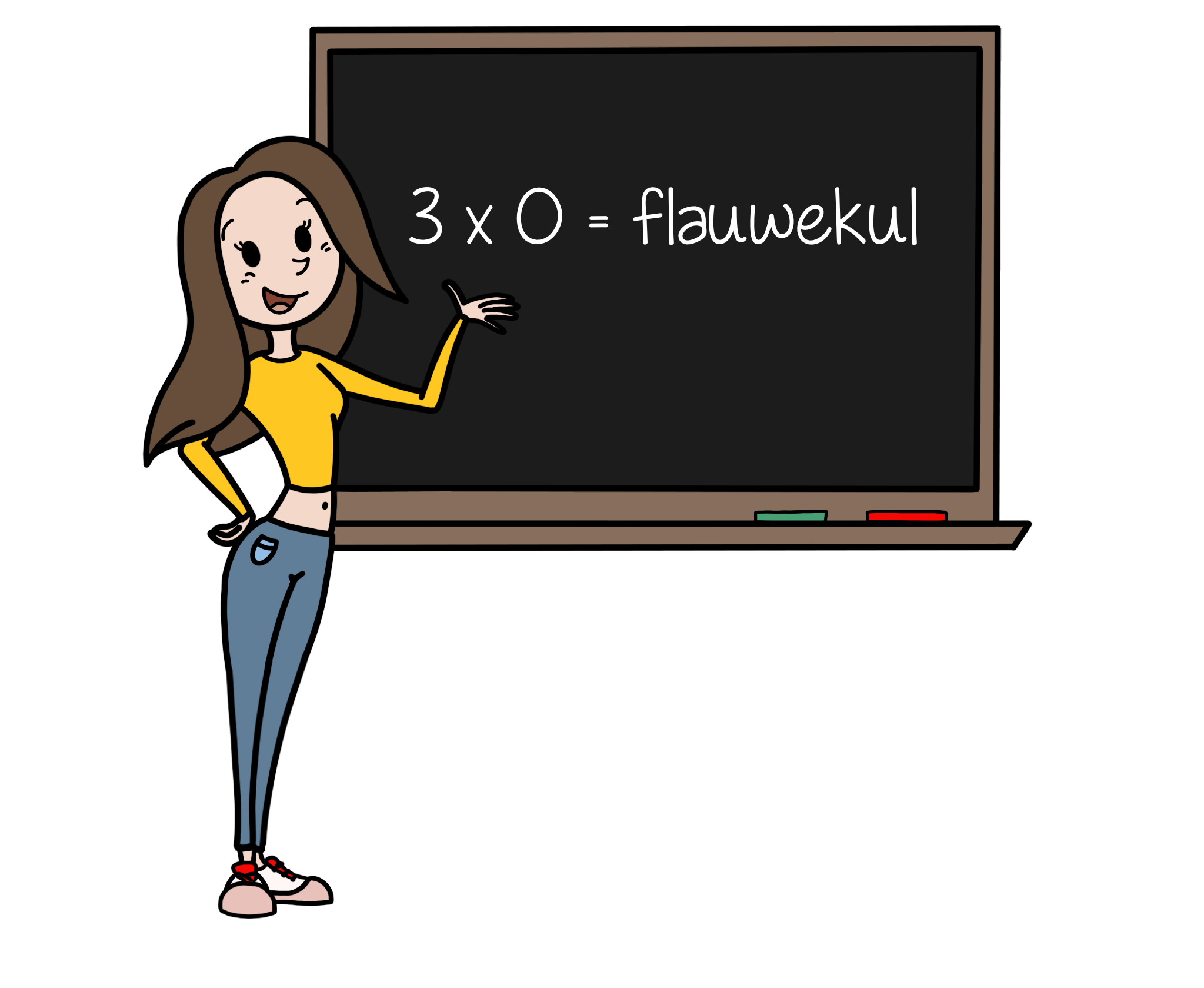
Tijdens het rekenonderwijs kunnen kinderen sommen tegenkomen waarbij meerdere bewerkingen nodig zijn.  Een ezelsbruggetje kan helpen om de volgorde waarin deze bewerkingen opgelost moeten worden, te onthouden.

Het ezelsbruggetje is de volgende zin: Hoe Moeten Wij Van De Onvoldoendes Afkomen?

Hoe = som tussen de Haakjes oplossen
Moeten = Machtsverheffen (7⁵ = 7 tot de macht 5)
Wij = Worteltrekken
Van = Vermenigvuldigen
De = Delen
Onvoldoendes = Optellen
Afkomen = Aftrekken

Inderdaad… deze volgorde is wat uitgebreider dan de vroegere ‘Meneer Van Dalen Wacht Op Antwoord’.

Rekenen met maten

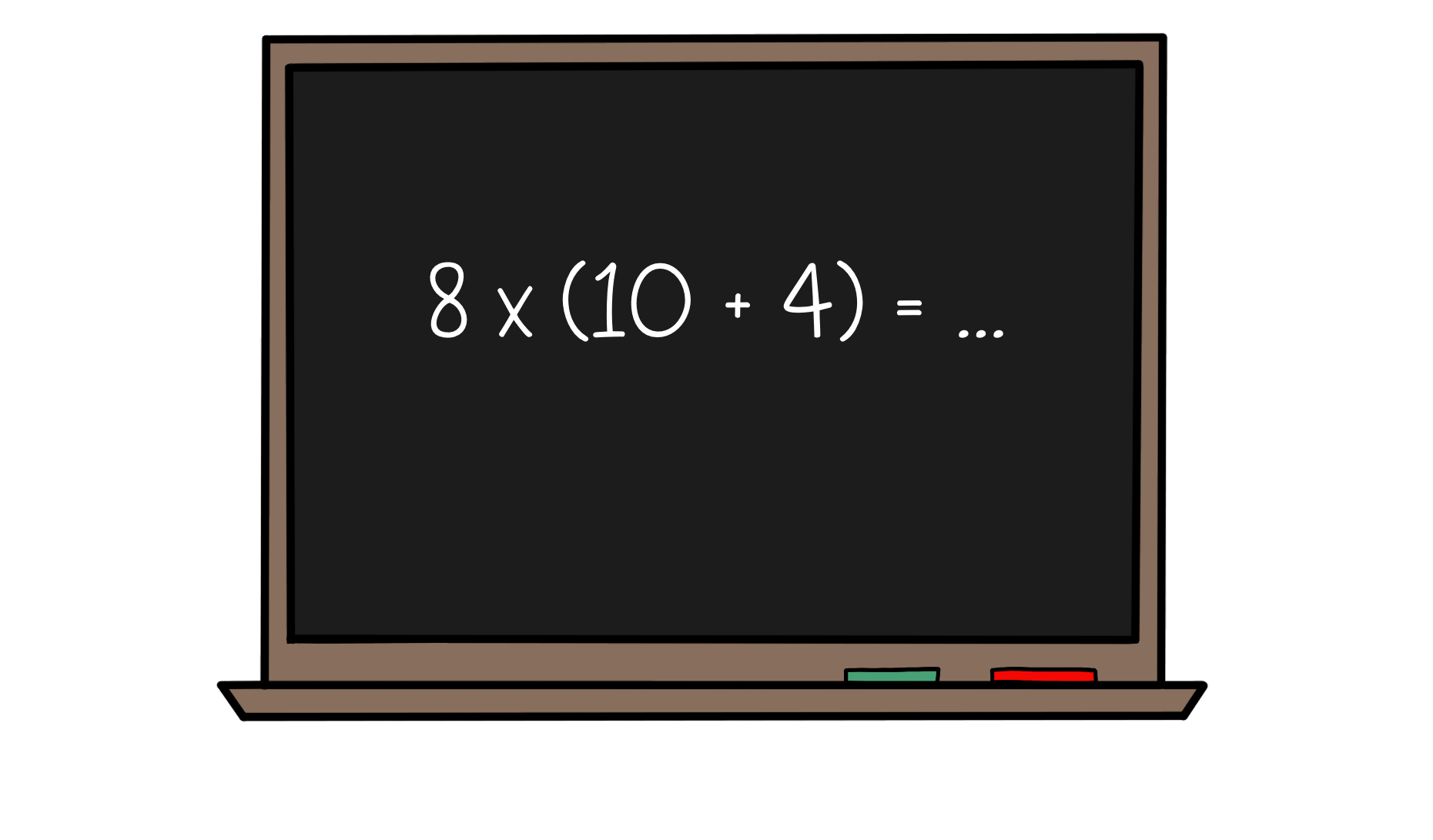
In de maatbeker zit 1 liter limonade. Hoeveel glazen van 250 milliliter kun je vullen?

Wanneer je gaat rekenen met maten, is het handig om dezelfde maat te gebruiken.

Een ezelsbruggetje dat je daarbij kunt gebruiken is: Als je rekenen gaat, gebruik dan dezelfde maat.

Niet alleen bij inhoudsmaten, maar ook bij het meten van een lengte, omtrek, oppervlakte of bij het rekenen met geld, is het handig om voor dezelfde maat te kiezen. Eerst even omrekenen dus!

Welk ezelsbruggetje gebruik jij? Laat het ons weten!

---

---

Hulp bij het rekenen: rekenvideo’s op Lesvananne.nl

Niet alle kinderen gaat het rekenen gemakkelijk af. Misschien heb je op school te horen gekregen, dat jouw kind moeite heeft met dit onderdeel van het rekenen. Of misschien heb je het zelf opgemerkt of heeft jouw kind zelf aangegeven het niet allemaal te begrijpen. Dan is het tijd om ermee aan de slag te gaan! En dat doe je zo!

Iets nieuws leren begint met het volgen van een instructie. Door onze instructievideo’s krijgt jouw kind de kans om de rekeninstructie, die ook op zijn/haar basisschool is gegeven, nog eens (of meerdere keren) te volgen. Door onze bijbehorende werkbladen kan jouw kind vervolgens nog eens met de leerstof oefenen. Voor veel kinderen maakt dit alleen al een enorm verschil! En dat is niet alles!

Elk kind leert op zijn eigen tempo en heeft zijn eigen niveau. Dit kan per rekencategorie erg verschillen. Het kan best zijn, dat jouw kind heel goed kan klokkijken, maar dat het automatiseren van de tafels maar niet lukt. Of dat de tafels er allang in zitten, maar het kwartje met betrekking tot breuken nog niet gevallen is. Dit is de reden dat jullie op ons platform toegang tot alle leerjaren van de basisschool krijgen. Jouw kind krijgt hierdoor ook de kans om de rekeninstructies van een leerjaar terug of een leerjaar verder te volgen. Iets waar de meeste basisscholen niet (consistent) in kunnen voorzien. Je kind werkt dus écht op zijn eigen tempo en op krijgt op zijn eigen niveau instructie. Dat is uniek en dé manier om zelfvertrouwen voor rekenen op te bouwen en de scores te verhogen.

Ga direct aan de slag en meld je hier aan!

---

Meteen zin in een instructieles over meten? In onderstaande les leert Anne je hoe je kunt meten in meters, centimeters en millimeters én leert ze je hoe je de maten naar elkaar kunt omrekenen. Veel rekenplezier!

Rekenvideo’s over meten

Wist je dat je op deze site allemaal instructievideo’s en bijpassende werkbladen over rekenen vindt? Hier vind je de lessen over het onderwerp ‘meten’ op een rij!

GROEP 3 LES 17 De meter

GROEP 4 LES 6 Meten met een meter
GROEP 4 LES 11 Meten met centimeters

GROEP 5 LES 2 Meter en centimeter
GROEP 5 LES 13 De kilometer
GROEP 5 LES 31 De omtrek
GROEP 5 LES 36 Meten in m, cm en mm
GROEP 5 LES 41 M² en cm²
GROEP 5 LES 47 De decimeter
GROEP 5 LES 51 Rekenen met m²

GROEP 6 LES 11 De trap met maten
GROEP 6 LES 13 Rekenen met schaal
GROEP 6 LES 37 Kaartlezen met schaal
GROEP 6 LES 42 Oppervlakte berekenen
GROEP 6 LES 55 Oppervlakte – kosten berekenen
GROEP 6 LES 56 Maten omrekenen
GROEP 6 LES 57 De omtrek – verschillende vormen
GROEP 6 LES 58 De oppervlakte – verschillende vormen
GROEP 6 LES 60 Inhoud berekenen met blokken

GROEP 7 LES 13 Afstanden berekenen met schaal
GROEP 7 LES 16 De m³, dm³ en cm³
GROEP 7 LES 21 Maten met kommagetal omrekenen
GROEP 7 LES 22 Oppervlaktematen omrekenen
GROEP 7 LES 31 Inhoudsmaten omrekenen
GROEP 7 LES 34 Inhoud berekenen
GROEP 7 LES 35 Inhoud vissenkom berekenen